Introductions to Psychometric Techniques: Differential Item Functioning, Part I: Introduction to Methods
Paragon Testing takes every aspect of test development and evaluation seriously. In order to help the interested reader understand some of the work that goes into ensuring that our tests are of the highest quality, this blog post series aims to provide an introduction to many of these aspects. This post is the first of two discussing differential item functioning. Part I provides an introduction to the topic. Part II provides an illustrative example of the DIF analyses that Paragon Testing conducts on a regular basis.
Background
The developers of psychosocial measures and tests have long been concerned with differential item functioning (hereafter referred to as DIF), and the field of language assessment is no exception. There is a large literature of DIF studies for high-stakes language proficiency tests (Young, et al., 2013; Aryadoust, Goh, & Kim, 2011; Zumbo, 2003; Ryan & Bachman, 1992). In language assessment DIF studies, the most common grouping variables are gender, language, and country of origin (Young et al., 2013). These variables are generally selected because they are of general interest or are known to be sources of possible DIF due to differing sociocultural backgrounds among test takers (Ferne & Rupp, 2007).
More generally, in any discussion of differential item functioning, it is important to note that DIF is not synonymous with bias or fairness. Questions of fairness in tests and measures are directly related to the use of an individual’s score on that test or measure. For example, if men and women from a given nation receive different levels of training in speaking English, whether and how scores on a speaking proficiency test should be used in making immigration decisions becomes a question of fairness. On the other hand, DIF analysis seeks to find out if men and women from that nation who are equally proficient in spite of unfair circumstances have an equal probability of answering a given test item correctly. Thus, DIF analysis is a step removed from external questions of bias and fairness in test decisions, but is instead concerned with the internal functioning of the test and test items. However, should a test or test item be found to exhibit DIF in favour of one group over another, this result may be relevant to any decision making process based on test scores, as well as a discussion of fairness regarding the use of that test.
Methods
A number of DIF analysis techniques have been developed, each of which has a variety strengths and weaknesses. Generally, however, the techniques can be divided along three types (Magis et al., 2010):
- Item Response Theory (IRT) based vs non-IRT based methods
IRT-based methods involve fitting models for the different groups under examination simultaneously to assess DIF between groups. This is a specific case of a generalized logistic model matching on theta, and IRT-based methods tends to be less straightforward to interpret (Zumbo, et al., 2015). Non-IRT based methods necessarily encompass all other methods of detecting DIF.
- Techniques which can detect uniform DIF, non-uniform DIF, or both
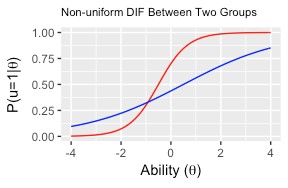
Uniform DIF is a pattern of DIF where the degree of DIF is constant across the spectrum of ability being assessed by a test, whereas non-uniform DIF acts as a function of both the degree of ability and the grouping variable. The contrast is displayed below. In Figure 1 the lines are parallel, with no change in slope over the spectrum of theta (test taker proficiency). In figure two, the lines are not parallel, and in fact cross one another. This indicates that difficulty of the item changes as a function of both group membership and theta level.
Figure 1:
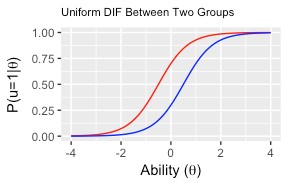 Figure 2:
Figure 2:
- Techniques which can make comparisons between two or more than two groups
The earliest techniques developed for detecting DIF, such as Mantel-Haenzel (MH), were capable of contrasting only two groups at once. For example, MH might be used to assess DIF between males and females, but it would require a number of pairwise comparisons to assess DIF between groups of males and females who varied on whether or not they had completed a university education.
Table 1 below shows the most common DIF analysis techniques and how they fit in these categories.
Table 1:
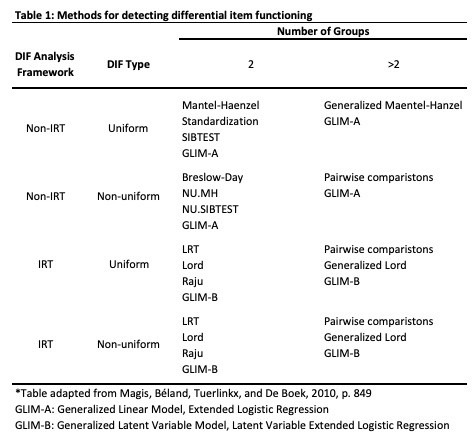
As can be seen above, only the logistic regression and generalized Lord techniques can be used to simultaneously detect both uniform and non-uniform DIF in more than two groups. The other techniques may be used in pairwise comparisons to search for DIF effects in multiple groups, at a cost. In using pairwise comparisons it is necessary to control for inflated significance levels using an alpha-correction technique such as a Bonferroni correction (Miller, 1981). In addition, according to Penfield (2001), pairwise comparison techniques tend to have lower power for detecting DIF than techniques which test all groups simultaneously.
In a recent survey of the most popular methods used in DIF studies (Moses, et al., 2010), logistic regression was shown to be the most broadly useful technique for analyzing DIF, as might be expected given that it is the only method belonging to each category in the table above — It is a special case general statistical modelling framework called the Generalized Linear Model, GLIM. In the case of the CELPIP test, this means that a single technique may be used for assessing DIF on all components of the CELPIP tests. Given these benefits, Logistic Regression has been selected as the method of choice for assessing DIF on the CELPIP tests in the present report.
References (Combined between Parts I and II)
Aryadoust, V., Goh, C. C. M., & Kim, L. O. (2011). An Investigation of Differential Item Functioning in the MELAB Listening Test. Language Assessment Quarterly, 8(4), 361–385. https://doi.org/10.1080/15434303.2011.628632
Ferne, T., & Rupp, A. A. (2007). A Synthesis of 15 Years of Research on DIF in Language Testing: Methodological Advances, Challenges, and Recommendations. Language Assessment Quarterly, 4(2), 113–148. https://doi.org/10.1080/15434300701375923
King, G., & Zeng, L. (2001). Logistic Regression in Rare Events Data. Political Analysis, 9(2), 137–163.
Jodoin, M. G., & Gierl, M. J. (2001). Evaluating Type I Error and Power Rates Using an Effect Size Measure With the Logistic Regression Procedure for DIF Detection. Applied Measurement in Education, 14(4), 329–349. https://doi.org/10.1207/S15324818AME1404_2
Lee, Y.-H., & Zhang, J. (2010). Differential Item Functioning: Its Consequences. ETS Research Report Series, 2010(1), i–25. https://doi.org/10.1002/j.2333-8504.2010.tb02208.x
Magis, D., Béland, S., Tuerlinckx, F., & De Boeck, P. (2010). A general framework and an R package for the detection of dichotomous differential item functioning. Behavior Research Methods, 42(3), 847–862. https://doi.org/10.3758/BRM.42.3.847
Miller, R. G. J. (1981). Simultaneous Statistical Inference (2nd ed.). New York: Springer-Verlag. Retrieved from //www.springer.com/gp/book/9781461381242
Moses, T., Miao, J., & Dorans, N. J. (2010). A Comparison of Strategies for Estimating Conditional DIF. Journal of Educational and Behavioral Statistics, 35(6), 726–743. https://doi.org/10.3102/1076998610379135
Penfield, R. D. (2001). Assessing Differential Item Functioning Among Multiple Groups: A Comparison of Three Mantel-Haenszel Procedures. Applied Measurement in Education, 14(3), 235–259. https://doi.org/10.1207/S15324818AME1403_3
Raju, N. S. (1988). The area between two item characteristic curves. Psychometrika, 53(4), 495–502. https://doi.org/10.1007/BF02294403
Ryan, K. E., & Bachman, L. F. (1992). Differential item functioning on two tests of EFL proficiency. Language Testing, 9(1), 12–29. https://doi.org/10.1177/026553229200900103
Shimizu, Y., & Zumbo, B. D. (2005). A Logistic Regression for Differential Item Functioning Primer. JLTA Journal, 7, 110–124. https://doi.org/10.20622/jltaj.7.0_110
Young, J. W., Morgan, R., Rybinski, P., Steinberg, J., & Wang, Y. (2013). Assessing the Test Information Function and Differential Item Functioning for the TOEFL Junior Standard Test. ETS Research Report Series, 2013(1), i–27. https://doi.org/10.1002/j.2333-8504.2013.tb02324.x
Zumbo, B. D., Thomas, D. R. (1997). A measure of effect size for a model-based approach for studying DIF. Prince George, Canada: University of Northern British Columbia, Edgeworth Laboratory for Quantitative Behavioural Science.
Zumbo, B. D. (1999). A Handbook on the Theory and Methods of Differential Item Functioning (DIF), 57.
Zumbo, B. D. (2003). Does item-level DIF manifest itself in scale-level analyses? Implications for translating language tests. Language Testing, 20(2), 136–147. https://doi.org/10.1191/0265532203lt248oa
Zumbo, B. D., Liu, Y., Wu, A. D., Shear, B. R., Olvera Astivia, O. L., & Ark, T. K. (2015). A Methodology for Zumbo’s Third Generation DIF Analyses and the Ecology of Item Responding. Language Assessment Quarterly, 12(1), 136–151. https://doi.org/10.1080/15434303.2014.972559


